对号函数,探索对号函数的奥秘与应用

你知道吗？在数学的世界里，有一种函数特别有趣，它就像一个顽皮的小精灵，总是能带来意想不到的惊喜。它就是——对号函数！今天，就让我带你一起探索这个神秘又迷人的数学世界，看看对号函数到底有哪些神奇之处吧！

对号函数的“真面目”

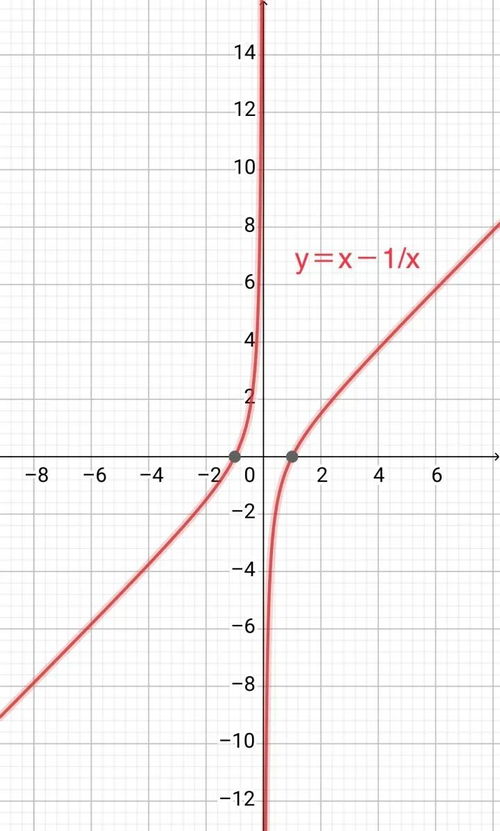
对号函数，学名叫作对勾函数，有时候还被称为双勾函数、勾函数、对号函数、双飞燕函数，甚至有个形象的名字叫“耐克函数”或“耐克曲线”。它的标准形式是 \\( f(x) = \\frac{ax}{bx} \\)，其中 \\( a \\) 和 \\( b \\) 是常数，而且 \\( a > 0 \\)，\\( b > 0 \\)。是不是觉得有点眼熟？没错，它就像我们熟悉的反比例函数，但又不完全一样。

对号函数的“性格特点”

1. 定义域：对号函数的定义域是所有非零实数，也就是说，它不能接受 \\( x = 0 \\) 这个“特殊”的数字。所以，它的定义域是 \\( (-\\infty, 0) \\cup (0, \\infty) \\)。

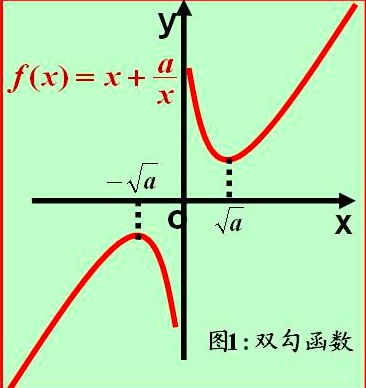
2. 值域：对号函数的值域有点特别，它分为两部分。当 \\( x > 0 \\) 时，值域是 \\( [2\\sqrt{ab}, \\infty) \\)；当 \\( x < 0 \\) 时，值域是 \\( (-\\infty, -2\\sqrt{ab}] \\)。是不是觉得有点像数学里的“对勾”？

3. 奇偶性：对号函数是个“调皮鬼”，它是个奇函数。也就是说，如果你把 \\( x \\) 替换成 \\( -x \\)，函数值会变成原来的相反数。

4. 单调性：对号函数在 \\( (-\\infty, -\\sqrt{\\frac{b}{a}}) \\) 和 \\( (\\sqrt{\\frac{b}{a}}, \\infty) \\) 上是单调递增的，在 \\( (-\\sqrt{\\frac{b}{a}}, \\sqrt{\\frac{b}{a}}) \\) 上是单调递减的。

5. 渐近线：对号函数的渐近线是 \\( y \\) 轴和直线 \\( y = ax \\)。当 \\( x \\) 趋向于正无穷或负无穷时，函数值会越来越接近这两条渐近线。

对号函数的“应用天地”

对号函数在数学的世界里可是个“多面手”，它不仅能解决一些复杂的不等式问题，还能在解决最值问题时大显身手。

1. 恒成立问题：比如，有一个函数 \\( f(x) = 3x^2 - tx 3 \\)，如果在区间 [1, 4] 上是单调递减的，那么我们可以利用对号函数的性质来解决这个问题。

2. 最值问题：对号函数的单调性可以帮助我们快速找到函数的最小值或最大值。

3. 实际问题：在物理学、经济学等领域，对号函数也有着广泛的应用。

对号函数的“学习小贴士”

1. 理解定义：首先要弄清楚对号函数的定义，这样才能更好地理解它的性质。

2. 掌握性质：对号函数的奇偶性、单调性、渐近线等性质是解决问题的关键。

3. 多做练习：只有通过大量的练习，才能真正掌握对号函数的应用。

4. 拓展思维：对号函数的应用非常广泛，要学会从不同角度去思考问题。

说了这么多，你是不是对对号函数有了更深的了解呢？这个数学世界里的“小精灵”是不是也让你感到好奇和兴奋呢？那就让我们一起继续探索吧！